分类： 赛事资讯

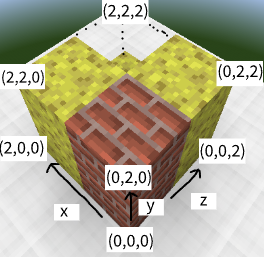
Farmer John has a block of cheese in the shape of a cube. It lies on the 3-dimensional coordinate plane, extending from (0,0,0)to (N,N,N) (2≤N≤1000). Farmer John will perform a series of Q (1≤Q≤2⋅10⁵) update operations to his cheese block.

For each update operation, FJ will carve out the 1 by 1 by 1 block of cheese extending from integer coordinates (x,y,z) to (x+1,y+1,z+1), where 0≤x,y,z<N. It is guaranteed that there will exist a 1 by 1 by 1block of cheese at the location FJ carves. Since FJ is playing Moocraft, gravity does not cause parts of the cheese to fall if cheese below is carved.

After each update, output the number of distinct configurations that FJ can stick a 1 by 1 by N brick in the cheese block such that no part of the brick overlaps with any remaining cheese. Every vertex of the brick must have integer coordinates in the range [0,N] for all three axes. FJ may rotate the brick however he wants.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains N and Q.

The following Q lines contain x, y, and z, the coordinates to be carved.

OUTPUT FORMAT (print output to the terminal / stdout):

After each update operation, output an integer, the number of configurations.

SAMPLE INPUT:

2 5
0 0 0
1 1 1
0 1 0
1 0 0
1 1 0

SAMPLE OUTPUT:

0
0
1
2
5

After the first three updates, the 1×2×1brick spanning [0,1]×[0,2]×[0,1] does not overlap with the remaining cheese, so it contributes toward the answer.

SCORING:

Inputs 2-4: N≤10 and Q≤1000
Inputs 5-7: N≤100 and Q≤1000
Inputs 8-16: No additional constraints

Problem credits: Chongtian Ma, Alex Liang

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Bessie the cow is back in school! She has started doing her math homework in which she is tasked to round positive integers to powers of 10.

To round a positive integer a to the nearest 10^b, where b is a positive integer, Bessie first locates the b'th digit from the right. Let x denote this digit.

If x ≥5, Bessie adds 10^b to a.

Then, Bessie sets all the digits including and to the right of the b'th digit from the right to be 0.

For instance, if Bessie wanted to round 456 to the nearest 10² (hundred), Bessie would first locate the 2nd digit from the right which is 5. This means x=5. Then since x≥5, Bessie adds 100 to a. Finally, Bessie sets all the digits in a to the right of and including the 2nd digit from the right to be 0, resulting in 500.

However, if Bessie were to round 446 to the nearest 102, she would end up with 400.

After looking at Bessie's homework, Elsie thinks she has invented a new type of rounding: chain rounding. To chain round to the nearest 10^b, Elsie will first round to the nearest 101, then the nearest 102, and so on until the nearest 10^b.

Bessie thinks Elsie is wrong, but is too busy with math homework to confirm her suspicions. She tasks you to count how many integers x at least 2 and at most N (1≤N≤10⁹) exist such that rounding x to the nearest 10^P is different than chain rounding to the nearest 10^P, where P is the smallest integer such that 10^P≥x.

INPUT FORMAT (input arrives from the terminal / stdin):

You have to answer multiple test cases.

The first line of input contains a single integer T(1≤T≤10⁵) denoting the number of test cases. T test cases follow.

The first and only line of input in every test case contains a single integer N. All N
within the same input file are guaranteed to be distinct.

OUTPUT FORMAT (print output to the terminal / stdout):

Output T lines, the i'th line containing the answer to the i'th test case. Each line should be an integer denoting how many integers at least 2 and at most N exist that are different when using the two rounding methods.

SAMPLE INPUT:

4
1
100
4567
3366

SAMPLE OUTPUT:

0
5
183
60

Consider the second test case in the sample. 48 should be counted because 48
chain rounded to the nearest 10² is 100(48→50→100), but 48rounded to the nearest 10² is 0.

In the third test case, two integers counted are 48 and 480. 48 chain rounds to 100 instead of to 0 and 480 chain rounds to 1000 instead of 0. However, 67 is not counted since it chain rounds to 100 which is 67rounded to the nearest 10².

SCORING:

Inputs 2-4: N≤10³
Inputs 5-7: N≤10⁶
Inputs 8-13: No additional constraints.

Problem credits: Weiming Zhou

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Farmer John's milk factory can be described by an N by N (1≤N≤1000) grid of cells that contain conveyor belts. Position (a,b) describes the cell that is in the a-th row from the top and b-th column from the left. There are 5 types of cells:

1."L" — the cell is a leftward facing conveyor belt which moves all items on it 1 cell left every time unit.
2."R" — the cell is a rightward facing conveyor belt which moves all items on it 1 cell right every time unit.
3."U" — the cell is an upward facing conveyor belt which moves all items on it 1 cell up every time unit.
4."D" — the cell is a downward facing conveyor belt which moves all items on it 1 cell down every time unit.
5."?" — Farmer John has not built a conveyor belt at that cell yet.

Note that conveyor belts can also move items outside the grid. A cell c is unusable if an item placed at cell c will never exit the conveyor belt grid (i.e. it will move around in the grid forever).

Initially, Farmer John has not started building the factory so all cells start out as "?". For the next Q (1≤Q≤2⋅10⁵) days starting from day 1 and ending at day Q
, Farmer John will choose a cell that does not have a conveyor belt and build a conveyor belt at the cell.

Specifically, during the i-th day, Farmer John will build a conveyor belt of type t_i (t_i ∈{L,R,U,D}) at position (r_i,c_i) (1≤r_i,c_i≤N). It is guaranteed that there is no conveyor belt at position (r_i,c_i).

After each day, help Farmer John find the minimum number of unusable cells he can achieve by optimally building conveyor belts on all remaining cells without a conveyor belt.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains N and Q .

The i-th of the next Q lines contains r_i, c_i, and t_i in that order.

OUTPUT FORMAT (print output to the terminal / stdout):

Q lines, the i-th of which describing the minimum number of unusable cells if Farmer John fills optimally builds conveyor belts on all remaining cells that do not currently have a conveyor belt.

SAMPLE INPUT:

3 5
1 1 R
3 3 L
3 2 D
1 2 L
2 1 U

SAMPLE OUTPUT:

0
0
0
2
3

The conveyor belt after the fifth day is shown below.
RL?
U??
?DL
One optimal way to build conveyor belts on the remaining cells is as follows.

RLR
URR
LDL

In this configuration, the cells at (1,1), (1,2), and (2,1) are unusable.

SAMPLE INPUT:

3 8
1 1 R
1 2 L
1 3 D
2 3 U
3 3 L
3 2 R
3 1 U
2 1 D

SAMPLE OUTPUT:

0
2
2
4
4
6
6
9

The conveyor belt after the eighth day is shown below.

RLD
D?U
URL

No matter what conveyor belt Farmer John can build at the center, all cells will be unusable.

SAMPLE INPUT:

4 13
2 2 R
2 3 R
2 4 D
3 4 D
4 4 L
4 3 L
4 2 U
3 1 D
4 1 R
2 1 L
1 1 D
1 4 L
1 3 D

SAMPLE OUTPUT:

0
0
0
0
0
0
0
0
11
11
11
11
13

SCORING:

Inputs 4-5: N≤10
Inputs 6-7: N≤40
Inputs 8-13: No additional constraints

Problem credits: Alex Liang

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Farmer John is expanding his farm! He has identified the perfect location in the Red-Black Forest, which consists of N trees (1≤N≤10⁵  ) on a number line, with the i-th tree at position x_i (−109≤x_i ≤10⁹).

Environmental protection laws restrict which trees Farmer John can cut down to make space for his farm. There are K restrictions (1≤K≤10⁵ ) specifying that there must always be at least t_i trees (1≤t_i ≤N) in the line segment [l_i,r_i]
, including the endpoints (−109≤l_i≤r_i≤10⁹). It is guaranteed that the Red-Black Forest initially satisfies these restrictions.

Farmer John wants to make his farm as big as possible. Please help him compute the maximum number of trees he can cut down while still satisfying all the restrictions!

INPUT FORMAT (input arrives from the terminal / stdin):

Each input consists of T (1≤T≤10) independent test cases. It is guaranteed that the sums of all N and of all K within an input each do not exceed 3⋅10⁵.

The first line of input contains T. Each test case is then formatted as follows:

The first line contains integers N and K.
The next line contains the N integers x₁,…,x_N.
Each of the next K lines contains three space-separated integers: l_i, r_i and t_i.

OUTPUT FORMAT (print output to the terminal / stdout):

For each test case, output a single line with an integer denoting the maximum number of trees Farmer John can cut down.

SAMPLE INPUT:

3
7 1
8 4 10 1 2 6 7
2 9 3
7 2
8 4 10 1 2 6 7
2 9 3
1 10 1
7 2
8 4 10 1 2 6 7
2 9 3
1 10 4

SAMPLE OUTPUT:

4
4
3

For the first test case, Farmer John can cut down the first 4 trees, leaving trees at

x_i = 2,6,7 to satisfy the restriction.

For the second test case, the additional restriction does not affect which trees Farmer John can cut down, so he can cut down the same trees and satisfy both restrictions.

For the third test case, Farmer John can only cut down at most 3 trees because there are initially 7 trees but the second restriction requires him to leave at least 4 trees uncut.

SCORING:

Input 2: N , K≤16
Inputs 3-5: N, K≤1000
Inputs 6-7:t_i=1 for all i=1,…,K.
Inputs 8-11: No additional constraints.

Problem credits: Tina Wang, Jiahe Lu, Benjamin Qi

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Bessie and Elsie have discovered a row of N cakes (2≤N≤5⋅10⁵ ,N even)
cakes, with sizes a₁,a₂,…,a_N in that order (1≤a_i≤10⁹).

Each cow wants to eat as much as possible. However, being very civilized cows, they decided to play a game to split it! The game proceeds with both cows alternating turns. Each turn consists of one of the following:

1.Bessie chooses two adjacent cakes and stacks them, creating a new cake with the sum of the sizes.
2.Elsie chooses either the leftmost or rightmost cake and puts it in her stash.

When only one cake remains, Bessie eats it, and Elsie eats all cakes in her stash. If both cows play optimally to maximize the amount of cake they eat and Bessie plays first, how much cake will each cow eat?

INPUT FORMAT (input arrives from the terminal / stdin):

Each input consists of T (1≤T≤10) independent test cases. It is guaranteed that the sum of all N within an input does not exceed 10⁶.

Each test case is formatted as follows. The first line contains N . The next line contains N space-separated integers, a₁,a₂,…,a_N.

OUTPUT FORMAT (print output to the terminal / stdout):

For each test case, output a line containing b and e, representing the amounts of cake Bessie and Elsie respectively will consume if both cows play optimally.

SAMPLE INPUT:

2
4
40 30 20 10
4
10 20 30 40

SAMPLE OUTPUT:

60 40
60 40

For the first test case, under optimal play,

1.Bessie will stack the middle two cakes. The cakes now have sizes [40,50,10].
2.Elsie will eat the leftmost cake. The remaining cakes now have sizes [50,10].
3.Bessie stacks the remaining two cakes.

Bessie will eat 30+20+10=60 cake, while Elsie will eat 40 cake.

The second test case is the reverse of the first, so the answer is the same.

SCORING:

Input 2: All a_i  are equal.
Input 3: N≤10
Inputs 4-7: N≤5000
Inputs 8-11: No additional constraints.

Problem credits: Linda Zhao, Agastya Goel, Gavin Ye

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Bessie the cow has N (1≤N≤2⋅10⁵) jobs for you to potentially complete. The i-th one, if you choose to complete it, must be started at or before time s_i and takes t_i time to complete (0≤s_i ≤10¹⁸,1≤t_i ≤10¹⁸).

What is the maximum number of jobs you can complete? Time starts at 0
, and once you start a job you must work on it until it is complete, without starting any other jobs in the meantime.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains T, the number of independent test cases (1≤T≤10). Each test case is formatted as follows.

The first line contains N.

Each of the next N lines contains two integers s_i and t_i . Row i+1 has the details for the ith job.

It is guaranteed that the sum of N over all test cases does not exceed 3⋅10⁵.

OUTPUT FORMAT (print output to the terminal / stdout):

For each test case, the maximum number of jobs you can complete, on a new line.

SAMPLE INPUT:

3
2
1 4
1 2
2
2 3
1 2
3
1 4
2 3
1 2

SAMPLE OUTPUT:

1
2
2

For the first test case, you can only complete one of the jobs. After completing one job, it will then be time 2 or later, so it is too late to start the other job, which must be started at time 1 or earlier.

For the second test case, you can start the second job at time 0 and finish at time 2, then start the first job at time 2 and finish at time 5.

SCORING:

Inputs 2: Within the same test case, all t_i  are equal.
Inputs 3-4: N≤2000, s_i ,t_i ≤2000
Inputs 5-8: N≤2000
Inputs 9-16: No additional constraints.

Problem credits: Benjamin Qi

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

It's the year 3000 , and Bessie became the first cow in space! During her journey between the stars, she found a number line with N (2≤N≤5⋅10⁵) points, numbered from 1 to N. All points are initially colored white. She can perform the following operation any number of times.

Choose a position i within the number line and a positive integer x. Then, color all the points in the interval [i,i+x−1] red and all points in [i+x , i+2x−1]
blue. All chosen intervals must be disjoint (i.e. no points in [ i, i+2x−1]
can be already colored red or blue). The entire interval must also fall within the number line (i.e. 1≤i≤i+2x−1≤N).

Farmer John gives Bessie a string s of length N consisting of characters R, B
, and X. The string represents Farmer John's color preferences for each point: s_i =R means the i'th point must be colored red, s_i =B means the i'th point must be colored blue, and s_i =X means there is no constraint on the color for the i'th point.

Help Bessie count the number of distinct ways for the number line to be colored while satisfying Farmer John's preferences. Two colorings are different if there is at least one corresponding point with a different color. Because the answer may be large, output it modulo 10⁹+7.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains an integer N.

The following line contains string s.

OUTPUT FORMAT (print output to the terminal / stdout):

Output the number of distinct ways for the number line to be colored while satisfying Farmer John's preferences modulo 10⁹+7.

SAMPLE INPUT:

6
RXXXXB

SAMPLE OUTPUT:

5

Bessie can choose i=1,x=1(i.e. color point 1 red and point 2 blue) and i=3,x=2
(i.e. color points 3,4 red and points 5,6 blue) to produce the coloring RBRRBB.

The other colorings are RRBBRB, RBWWRB, RRRBBB, and RBRBRB.

SAMPLE INPUT:

6
XXRBXX

SAMPLE OUTPUT:

6

The six colorings are WWRBWW, WWRBRB, WRRBBW, RBRBWW, RBRBRB, and RRRBBB.

SAMPLE INPUT:

12

XBXXXXRXRBXX

SAMPLE OUTPUT:

18

SCORING:

Input 4: N≤500
Inputs 5-6: N≤10⁴
Inputs 7-13: All but at most 100 characters in s are X.
Inputs 14-23: No additional constraints

Problem credits: Chongtian Ma, Alex Liang

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Farmer John's N (1≤N≤10⁵ ) cows have been arranged into a line. The i
th cow has label a_i (1≤a_i ≤N). A group of cows can form a friendship group if they all have the same label and each cow is within x cows of all the others in the group, where x is an integer in the range [1,N]. Every cow must be in exactly one friendship group.

For each x from 1 to N , calculate the minimum number of friendship groups that could have formed.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line consists of an integer N.

The next line contains a₁...a_N , the labels of each cow.

OUTPUT FORMAT (print output to the terminal / stdout):

For each x from 1 to N , output the minimum number of friendship groups for that x on a new line.

SAMPLE INPUT:

9
1 1 1 9 2 1 2 1 1

SAMPLE OUTPUT:

7
5
4
4
4
4
4
3
3

Here are examples of how to assign cows to friendship groups for x=1
and x=2 in a way that minimizes the number of groups. Each letter corresponds to a different group.

SCORING:

Inputs 2-3: N≤5000
Inputs 4-7: a_i≤10 for all i
Inputs 8-11: No label appears more than 10 times.
Inputs 12-20: No additional constraints.

Problem credits: Chongtian Ma

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Moo! You are given an integer N (2≤N≤2000). Consider all permutations p=[p₀,p₁,…,p_N−1]of [0,1,2…,N−1]. Let f(p)=|p_i−p_i+1|denote the minimum absolute difference between any two consecutive elements of p. and let S denote the set of all p that achieve the maximum possible value of f(p).

You are additionally given K (0≤K≤N) constraints of the form p_i=j (0≤i, j<N). Count the number of permutations in S satisfying all constraints, modulo 10⁹+7.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains T (1≤TN≤2⋅10⁴) and N, meaning that you will need to solve T independent test cases, each specified by a different set of constraints.

Each test case starts with K, followed by K lines each containing i and j. It is guaranteed that

The same i does not appear more than once within the same test case.
The same j does not appear more than once within the same test case.

OUTPUT FORMAT (print output to the terminal / stdout):

For each test case, the answer modulo 10⁹+7 on a separate line.

SAMPLE INPUT:

3 4
0
1
1 1
2
0 2
2 3

SAMPLE OUTPUT:

2
0
1

The maximum possible value of f (p) is 2, and S={[2,0,3,1],[1,3,0,2]}.

SAMPLE INPUT:

9 11
2
0 5
6 9
3
0 5
6 9
1 0
4
0 5
6 9
1 0
4 7
5
0 5
6 9
1 0
4 7
2 6
6
0 5
6 9
1 0
4 7
2 6
9 3
7
0 5
6 9
1 0
4 7
2 6
9 3
5 2
8
0 5
6 9
1 0
4 7
2 6
9 3
5 2
7 4
9
0 5
6 9
1 0
4 7
2 6
9 3
5 2
7 4
3 1
10
0 5
6 9
1 0
4 7
2 6
9 3
5 2
7 4
3 1
8 10

SAMPLE OUTPUT:

6
6
1
1
1
1
1
1
1

p=[5,0,6,1,7,2,9,4,10,3,8] should be counted for all test cases.

SAMPLE INPUT:

10 11
0
1
3 8
2
3 8
5 7
3
3 8
5 7
4 2
4
3 8
5 7
4 2
10 6
5
3 8
5 7
4 2
10 6
8 10
6
3 8
5 7
4 2
10 6
8 10
1 9
7
3 8
5 7
4 2
10 6
8 10
1 9
7 5
8
3 8
5 7
4 2
10 6
8 10
1 9
7 5
2 3
9
3 8
5 7
4 2
10 6
8 10
1 9
7 5
2 3
6 0

SAMPLE OUTPUT:

160
20
8
7
2
1
1
1
1
1

p=[4,9,3,8,2,7,0,5,10,1,6]should be counted for all test cases.

SAMPLE INPUT:

5 987
3
654 321
543 210
432 106
2
654 321
543 210
1
654 321
1
0 493
0

SAMPLE OUTPUT:

0
538184948
693625420
932738155
251798971
Make sure to output the answer modulo 10⁹+7.

SCORING:

Input 5: N=15
Input 6: N=2000
Inputs 7-9: For all test cases, the constraint p₀=⌊N/2⌋ appears.
Inputs 10-13: For all test cases, there exists some constraint p_i =j with j equal to ⌊N/2⌋.
Inputs 14-20: No additional constraints.

Problem credits: Benjamin Qi

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划

Bessie has a string of length N(1≤N≤3⋅10⁵) consisting solely of the characters M and O. For each position i of the string, there is a cost c_i to change the character at that position to the other character (1≤c_i≤10⁸).

Bessie thinks the string will look better if it contains more moos of length L
(1≤L≤min(N,3)). A moo of length L is an M followed by L−1 Os.

For each positive integer k from 1 to ⌊N/L⌋ inclusive, compute the minimum cost to change the string to contain at least k substrings equal to a moo of length L.

INPUT FORMAT (input arrives from the terminal / stdin):

The first line contains L and N.

The next line contains Bessie's length-N string, consisting solely of Ms and Os.

The next line contains space-separated integers c₁…c_N.

OUTPUT FORMAT (print output to the terminal / stdout):

Output ⌊N/L⌋ lines, the answer for each k in increasing order.

SAMPLE INPUT:

1 4
MOOO
10 20 30 40

SAMPLE OUTPUT:

0
20
50
90

SAMPLE INPUT:

3 4
OOOO
50 40 30 20

SAMPLE OUTPUT:

40

SAMPLE INPUT:

2 20
OOOMOMOOOMOOOMMMOMOO
44743602 39649528 94028117 50811780 97338107 30426846 94909807 22669835 78498782 18004278 16633124 24711234 90542888 88490759 12851185 74589289 54413775 21184626 97688928 10497142

SAMPLE OUTPUT:

0
0
0
0
0
12851185
35521020
60232254
99881782
952304708

SAMPLE INPUT:

3 20
OOOMOMOOOMOOOMMMOMOO
44743602 39649528 94028117 50811780 97338107 30426846 94909807 22669835 78498782 18004278 16633124 24711234 90542888 88490759 12851185 74589289 54413775 21184626 97688928 10497142

SAMPLE OUTPUT:

0
0
0
44743602
119332891
207066974

SCORING:

Input 5: L=3,N≤5000
Input 6: L=1
Inputs 7-10: L=2
Inputs 11-18: L=3

Problem credits: Benjamin Qi

扫码领取USACO试题答案+详细解析

咨询一对一备赛规划