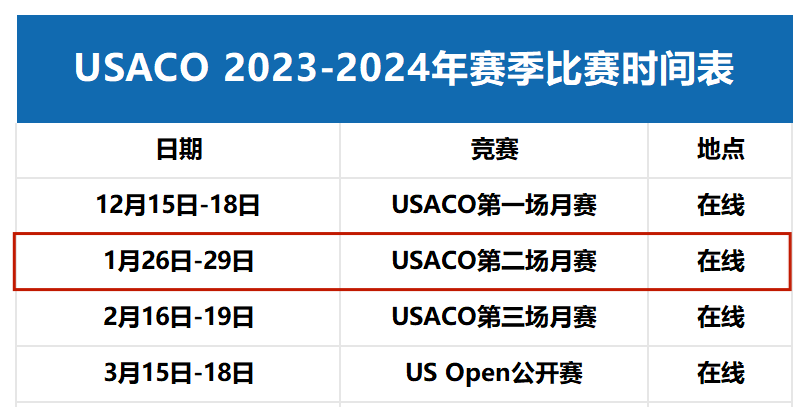
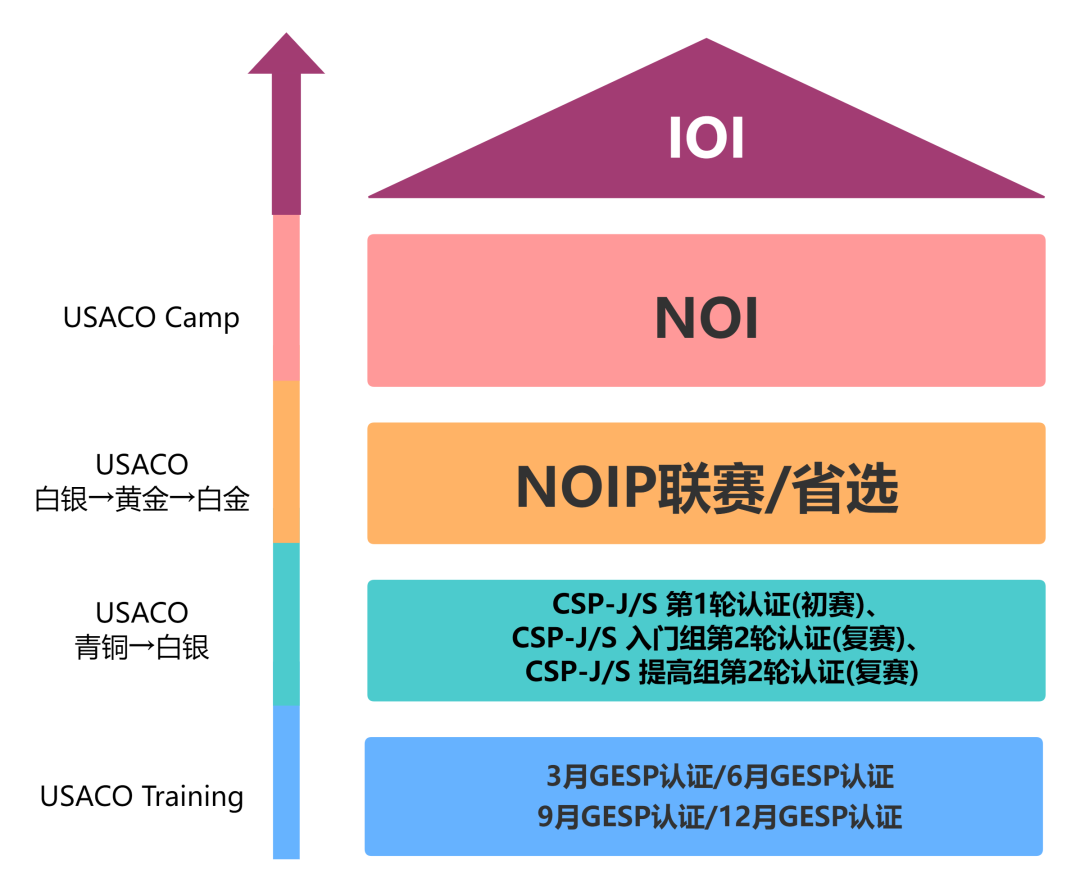
参与编程竞赛在计算机科学和软件工程领域中具有重要性。参赛者可以培养解决问题的能力、算法设计与优化技能,并提高编程效率。USACO竞赛经验对于就业和升学都具有很大的帮助。
USACO适合几年级?什么基础?
USACO竞赛适合中学阶段的学生参加。一般来说,学生在初中或高中阶段开始学习编程和算法,并且具备一定的编程基础和算法知识,就可以考虑参加USACO竞赛。
USACO同一场比赛可多次参加?
一个选手应该使用唯一的账号,每场比赛同一级别最多参加一次。使用多账号参加多次等行为属于作弊,将面临终身赛的惩罚。
如果选手第一个月比赛中没有成功晋级,并不影响之后参加第二个月的比赛,不过会因此增加一个月的晋级等待时间。
对于USACO竞赛的基础要求,可以根据学生的情况进行选择:
刚入门编程的学生:如果学生刚刚开始学习编程,对于USACO竞赛来说,需要学习编程的基础知识,如变量、条件语句、循环、函数等。此时,可以选择学习一门编程语言,如Python,作为入门语言,并通过学习编程教材和参加编程培训班等方式,掌握基本的编程概念和技巧。
具有一定算法基础的学生:如果学生已经具备一定的算法基础,熟悉常见的算法和数据结构,可以考虑配置NOIP(全国青少年信息学奥林匹克联赛)和USACO竞赛。NOIP竞赛要求使用C++语言,因此学生需要掌握C++语言的基础知识和编程技巧。USACO竞赛可以使用多种编程语言,包括Python和C++等。
之前学习了其他编程语言的学生:如果学生之前学习了除了C++以外的其他编程语言,可以选择参加USACO竞赛。USACO竞赛可以使用多种编程语言,因此学生可以继续使用之前学过的编程语言参加竞赛。
USACO竞赛适合中学阶段的学生参加,要求学生具备一定的编程基础和算法知识。根据学生的情况,可以选择合适的编程语言和竞赛配置,通过学习和练习提高自己的编程能力和解题能力。
扫码免费领取USACO知识点思维导图 + 备考书单


USACO竞赛冬季班课开启,提前锁定席位,扫码了解课程详情!