USACO在美国大学申请过程中具有非常高的含金量和竞争力,在比赛中取得优异成绩有助于申请美国的顶尖大学,特别是在计算机专业方面。越来越多进入哈佛、耶鲁、麻省理工学院、普林斯顿和康奈尔等顶尖大学的学生都曾参加过USACO,并且取得了非常出色的成绩。
目前,USACO竞赛在美国名校中非常受欢迎,但在中国选手中的影响力相对较小。然而,由于USACO竞赛的历史悠久和题目质量很高,它有可能在未来一两年内逐渐像AMC竞赛一样变得非常热门。
USACO竞赛的获奖难度如何?
USACO竞赛的获奖难度相对较高。根据历年的数据,能够晋级到白金级别的中国选手数量很少,通常只有几十人左右。而在白金级别中获得满分的中国选手数量通常在0到10人之间。
USACO竞赛近些年参赛人数暴增,参考2022-2023赛季,中国参赛总人数为10399人,每场比赛中,中国参赛者占比在27%-36%之间,仅次于美国,位居第二。
月赛:初始注册USACO账号即可达到铜级,铜升银比率为15%, 白银升黄金比率为12%,黄金升铂金比率为8%。
正因为如此,USACO竞赛的含金量非常高,难度也非常大。然而,USACO竞赛的好处是比较开放,学生可以通过系统的辅导和训练来获得高分和快速晋级。通过一段时间的努力,获得白银和黄金级别是有可能的。
USACO竞赛结果如何查询?
代码提交后,系统会自动给出评分,如果拿到了满分,系统会提示直接晋级。
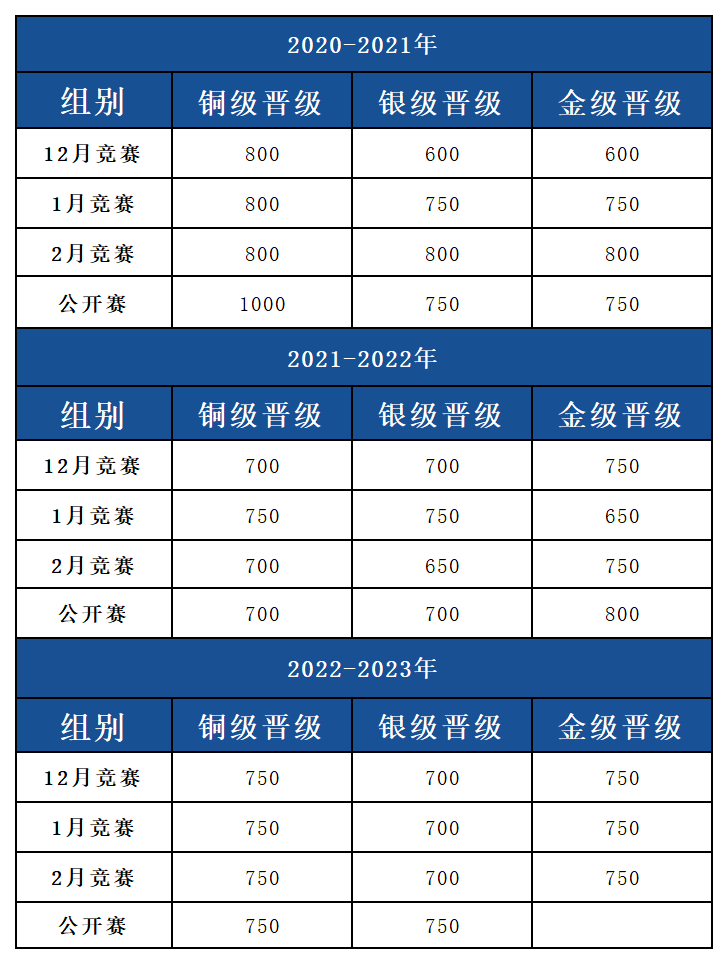
如果没有拿到满分,需要等待官方公布晋级分数线,每场月赛结束后一周内,官方会通过电子邮箱发放参赛选手的程序的评测结果。成功晋级就可以在下一场月赛中参加更高级别的竞赛,没有成功晋级只能在下一场月赛中继续在原组别中打比赛。
同时进入官网,点击Contests,在相应的页面上可以找到比赛的最终结果总结、测试数据、题目解析、比赛的简要分析及参赛选手的成绩统计。
USACO学术活动长线备考班、冲刺班已开启,扫描文末二维码领取限时优惠及备赛真题资料~
USACO秋季课程 正在火热组班中
金牌导师&精编讲义“强强联手”