**Note: The memory limit for this problem is 512MB, twice the default.**
Bessie is having fun playing a famous online game, where there are a bunch of cells of different labels and sizes. Cells get eaten by other cells until only one winner remains.
There are N (2≤N≤5000) cells in a row labeled 1…N from left to right, with initial sizes s1,s2,…,sN (1≤si≤105). While there is more than one cell, a pair of adjacent cells is selected uniformly at random and merged into a single new cell according to the following rule:
If a cell with label a and current size ca is merged with a cell with label b and current size cb , the resulting cell has size ca +cb and label equal to that of the larger cell, breaking ties by larger label. Formally, the label of the resulting cell is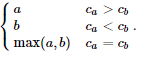 
For each label i in the range 1…N , the probability that the final cell has label i
can be expressed in the form 
where bi≢0 ( mod 109+7). Output aib−1i ( mod 109+7).
INPUT FORMAT (input arrives from the terminal / stdin):
The first line contains N.
The next line contains s1,s2,…,sN
OUTPUT FORMAT (print output to the terminal / stdout):
The probability of the final cell having label i modulo 109+7
for each i in 1…N on separate lines.
SAMPLE INPUT:
3
1 1 1
SAMPLE OUTPUT:
0
500000004
500000004
There are two possibilities, where (a,b)→c means that the cells with labels a and b merge into a new cell with label c.
(1, 2) -> 2, (2, 3) -> 2
(2, 3) -> 3, (1, 3) -> 3
So with probability 1/2 the final cell has label 2 or 3.
SAMPLE INPUT:
4
3 1 1 1
SAMPLE OUTPUT:
666666672
0
166666668
166666668
The six possibilities are as follows:
(1, 2) -> 1, (1, 3) -> 1, (1, 4) -> 1
(1, 2) -> 1, (3, 4) -> 4, (1, 4) -> 1
(2, 3) -> 3, (1, 3) -> 1, (1, 4) -> 1
(2, 3) -> 3, (3, 4) -> 3, (1, 3) -> 3
(3, 4) -> 4, (2, 4) -> 4, (1, 4) -> 4
(3, 4) -> 4, (1, 2) -> 1, (1, 4) -> 1
So with probability 2/3 the final cell has label 1, and with probability 1/6
the final cell has label 3 or 4.
SCORING:
Input 3: N≤8
Inputs 4-8: N≤100
Inputs 9-14: N≤500
Inputs 15-22: No additional constraints.
Problem credits: Benjamin Qi
扫码领取USACO试题答案+详细解析
咨询一对一备赛规划
